Blocking in experimental design
Table Of Content

The plot of residuals versus order sometimes indicates a problem with the independence assumption. Another way to look at these residuals is to plot the residuals against the two factors. Notice that pressure is the treatment factor and batch is the block factor. Both the treatments and blocks can be looked at as random effects rather than fixed effects, if the levels were selected at random from a population of possible treatments or blocks.
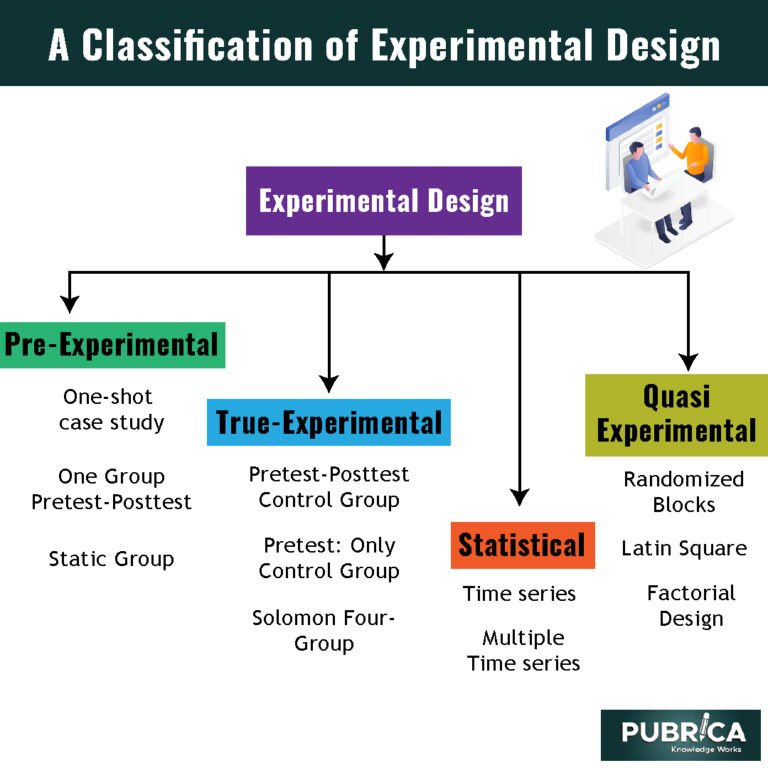
7 - Incomplete Block Designs
There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. So I decided to look back at the fishbone diagram to find some new variables to consider, ones that I cannot manipulate. You can obtain the 'least squares means' from the estimated parameters from the least squares fit of the model. My guess is that they all started the experiment at the same time - in this case, the first model would have been appropriate.
Other Aspects of the RCBD
Tesla experiments with interesting Supercharger lot design in Denmark - TESLARATI
Tesla experiments with interesting Supercharger lot design in Denmark.
Posted: Thu, 05 Jan 2023 08:00:00 GMT [source]
However, this method of constructing a BIBD using all possible combinations, does not always work as we now demonstrate. If the number of combinations is too large then you need to find a subset - - not always easy to do. However, sometimes you can use Latin Squares to construct a BIBD. As an example, let's take any 3 columns from a 4 × 4 Latin Square design. This subset of columns from the whole Latin Square creates a BIBD. With our first cow, during the first period, we give it a treatment or diet and we measure the yield.
Beyond A/B Testing: Primer on Causal Inference - Towards Data Science
Beyond A/B Testing: Primer on Causal Inference.
Posted: Fri, 28 Feb 2020 08:00:00 GMT [source]
Crossover Design Balanced for Carryover Effects
An assumption that we make when using a Latin square design is that the three factors (treatments, and two nuisance factors) do not interact. If this assumption is violated, the Latin Square design error term will be inflated. The Latin Square Design gets its name from the fact that we can write it as a square with Latin letters to correspond to the treatments. The treatment factor levels are the Latin letters in the Latin square design. The number of rows and columns has to correspond to the number of treatment levels. So, if we have four treatments then we would need to have four rows and four columns in order to create a Latin square.
Here are some examples of what your blocking factor might look like. By extension, note that the trials for any K-factor randomized block design are simply the cell indices of a k dimensional matrix. After I promised an introduction to blocking in design of experiments last time, one of our Minitab statisticians came to see me.
This situation can be represented as a set of 5, 2 × 2 Latin squares. And the 12 machines are distinguished by nesting the i index within the h replicates. Here is a plot of the least squares means for Yield with all of the observations included. Above you have the least squares means that correspond exactly to the simple means from the earlier analysis.
If both the machine and the operator have an effect on the time to produce, then by using a Latin Square Design this variation due to machine or operators will be effectively removed from the analysis. At a high level, blocking is used when you are designing a randomized experiment to determine how one or more treatments affect a given outcome. More specifically, blocking is used when you have one or more key variables that you need to ensure are similarly distributed within your different treatment groups. An alternate way of summarizing the design trials would be to use a 4x3 matrix whose 4 rows are the levels of the treatment X1 and whose columns are the 3 levels of the blocking variable X2. The cells in the matrix have indices that match the X1, X2 combinations above. Blocking is a technique used in design of experiments methodology to deal with the systematic differences to ensure that all the factors of interest and interactions between the factors can be assessed in the design.
Because the specific details of how blocking is implemented can vary a lot from one experiment to another. For that reason, we will start off our discussion of blocking by focusing on the main goal of blocking and leave the specific implementation details for later. You can see this by these contrasts - the comparison between block 1 and Block 2 is the same comparison as the AB contrast.
Blocking allows us to account for these differences, even when we can’t manipulate—or even measure—the variables. There are, of course, experiments in which you can manipulate or accurately measure temperature and humidity, but I’m not in such an environment. In fact, while I could get ambient weather information for my area, I don't even have a thermometer or hygrometer in my office. What I’d most like to do is get all of my measurements under fairly stable conditions so that I could assume that temperature and humidity affect every gummi bear launch the same way.
By blocking on sex, this source of variability is controlled, therefore, leading to greater interpretation of how the diet pills affect weight loss. In general, we are faced with a situation where the number of treatments is specified, and the block size, or number of experimental units per block (k) is given. This is usually a constraint given from the experimental situation. And then, the researcher must decide how many blocks are needed to run and how many replicates that provides in order to achieve the precision or the power that you want for the test.
A nuisance factor is a factor that has some effect on the response, but is of no interest to the experimenter; however, the variability it transmits to the response needs to be minimized or explained. We will talk about treatment factors, which we are interested in, and blocking factors, which we are not interested in. We will try to account for these nuisance factors in our model and analysis. To address nuisance variables, researchers can employ different methods such as blocking or randomization. Blocking involves grouping experimental units based on levels of the nuisance variable to control for its influence. Randomization helps distribute the effects of nuisance variables evenly across treatment groups.
Comments
Post a Comment