7 4: Blocking in 2 Dimensions Latin Square Statistics LibreTexts
Table Of Content
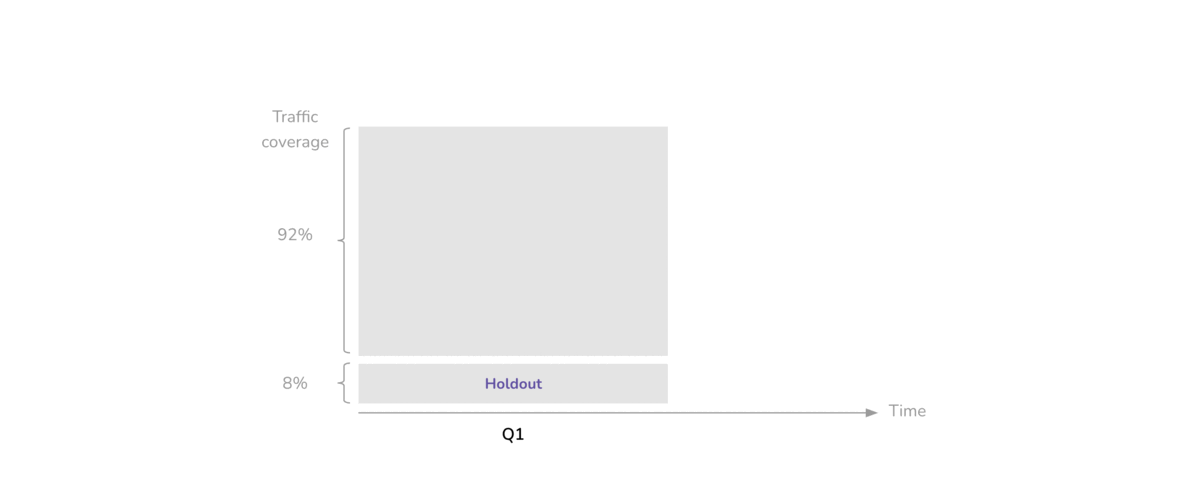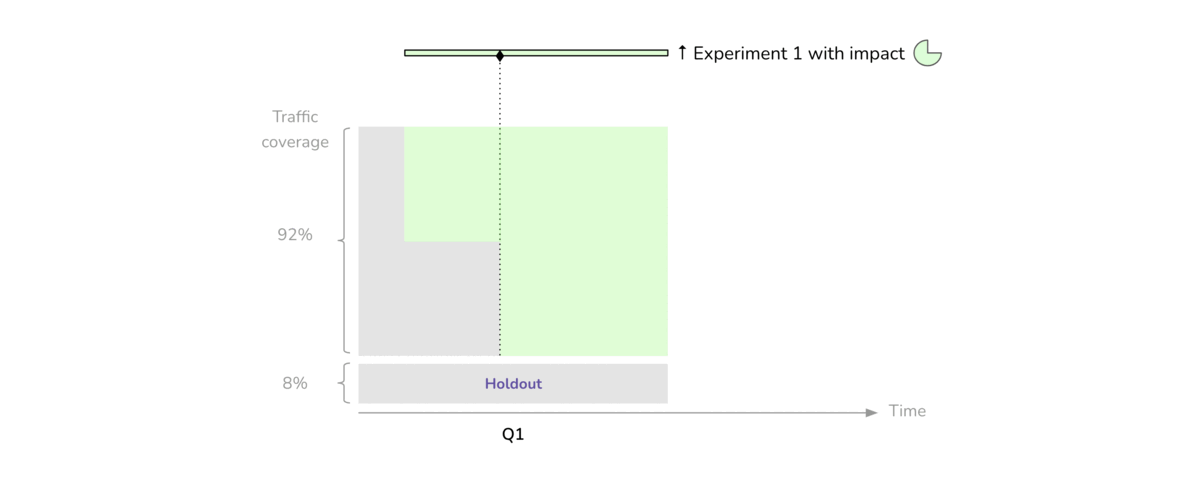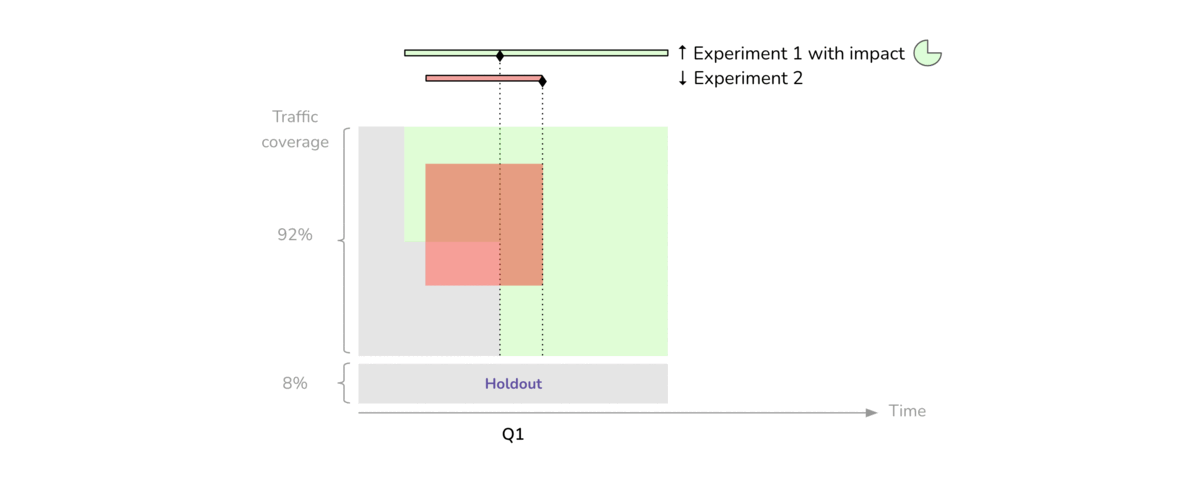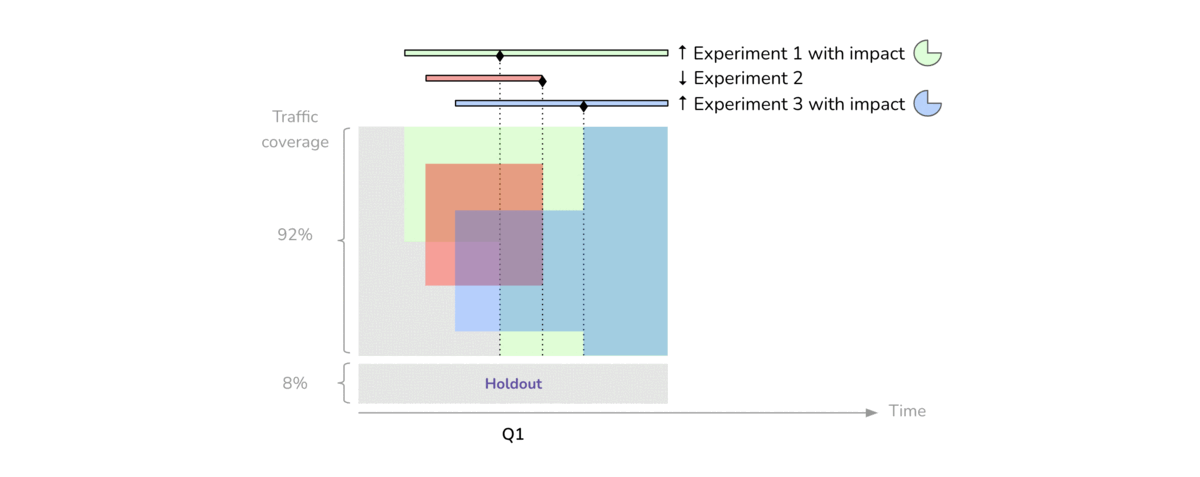
In the experiment we’re planning with the gummi bears, we’ll use blocks to account for data collected on different days. We’ll also use blocks to try to avoid a fatigue effect on the catapult. From doing this experiment with classes that I teach, I’m pretty confident that in 20 runs there won’t be noticeable fatigue.
Table of Contents
This property has an impact on how we calculate means and sums of squares, and for this reason, we can not use the balanced ANOVA command in Minitab even though it looks perfectly balanced. We will see later that although it has the property of orthogonality, you still cannot use the balanced ANOVA command in Minitab because it is not complete. After calculating x, you could substitute the estimated data point and repeat your analysis. So you can analyze the resulting data, but now should reduce your error degrees of freedom by one. In any event, these are all approximate methods, i.e., using the best fitting or imputed point. Suppose that there are a treatments (factor levels) and b blocks.
ANOVA Display for the RCBD
The single design we looked at so far is the completely randomized design (CRD) where we only have a single factor. In the CRD setting we simply randomly assign the treatments to the available experimental units in our experiment. Ideally, experiments should be run by using completely randomized experimental units. However, often, there is not enough experimental units from one homogenous sample.
Why is the randomized controlled double-blind experiment ideal?
Single 5 μm diameter needle electrode block modules for unit recordings in vivo Scientific Reports - Nature.com
Single 5 μm diameter needle electrode block modules for unit recordings in vivo Scientific Reports.
Posted: Tue, 25 Oct 2016 07:00:00 GMT [source]
Different batches do not necessarily mean non-homogeneity all the time. However, keeping track of the batch numbers as blocks (the statistical term) would provide an opportunity, if in case there is non-homogeneity from batch to batch. Therefore, a block is defined by a homogenous large unit, including, raw materials, areas, places, plants, animals, humans, etc. where samples or experimental units drawn are considered identical twins, but independent. The choice of case depends on how you need to conduct the experiment. If you are simply replicating the experiment with the same row and column levels, you are in Case 1.
If you are changing one or the other of the row or column factors, using different machines or operators, then you are in Case 2. If both of the block factors have levels that differ across the replicates, then you are in Case 3. The third case, where the replicates are different factories, can also provide a comparison of the factories. The fact that you are replicating Latin Squares does allow you to estimate some interactions that you can't estimate from a single Latin Square. If we added a treatment by factory interaction term, for instance, this would be a meaningful term in the model, and would inform the researcher whether the same protocol is best (or not) for all the factories.
Analysis of BIBD's
In the 2k design of experiment, blocking technique is used when enough homogenous experimental units are not available. Latin Square Designs are probably not used as much as they should be - they are very efficient designs. In other words, these designs are used to simultaneously control (or eliminate) two sources of nuisance variability.
Obviously, you don't have any carryover effects here because it is the first period. However, what if the treatment they were first given was a really bad treatment? In fact in this experiment the diet A consisted of only roughage, so, the cow's health might in fact deteriorate as a result of this treatment.
We give the treatment, then we later observe the effects of the treatment. This is followed by a period of time, often called a washout period, to allow any effects to go away or dissipate. This is followed by a second treatment, followed by an equal period of time, then the second observation. We let the row be the machines, the column be the operator, (just as before) and the Greek letter the day, (you could also think of this as the order in which it was produced).
Therefore the Greek letter could serve the multiple purposes as the day effect or the order effect. The numerator of the F-test, for the hypothesis you want to test, should be based on the adjusted SS's that is last in the sequence or is obtained from the adjusted sums of squares. That will be very close to what you would get using the approximate method we mentioned earlier.
A similar exercise can be done to illustrate the confounded situation where the main effect, say A, is confounded with blocks. Again, since this is a bit nonstandard, we will need to generate a design in Minitab using the default settings and then edit the worksheet to create the confounding we desire and analyze it in GLM. In addition you can open this Minitab project file 2-k-confound-ABC.mpx and review the steps leading to the output. The response variable Y is random data simply to illustrate the analysis.
Consider a factory setting where you are producing a product with 4 operators and 4 machines. Then you can randomly assign the specific operators to a row and the specific machines to a column. The treatment is one of four protocols for producing the product and our interest is in the average time needed to produce each product.
Comments
Post a Comment